Enhancing Feature Optimization for Crop Yield Prediction Models

Introduction

In the agricultural sector, precise crop yield prediction is essential because it directly affects food security and economic stability. The agricultural yield production is influenced significantly by various factors such as weather conditions, pest infestations, and the planning of harvest operations.¹ Therefore, accurate yield prediction is crucial for making well-informed decisions regarding agricultural risk management. Early yield prediction allows farmers to take precautionary measures to enhance productivity.² This prediction is feasible by collecting and analyzing data on historical farming experiences, weather conditions, soil parameters, water availability, and other critical factors such as rainfall, temperature, humidity, solar radiation, crop population density, fertilizer application, irrigation practices, tillage methods, soil type, soil depth, farm capacity, and soil organic matter.³ Simplifying prediction models necessitates the selection of important, non-redundant attributes from large datasets using feature selection techniques.⁴ The main objective of feature selection is eliminating irrelevant attributes to reduce analysis time and improve prediction accuracy. Implementing feature selection on the original dataset boosts the performance of crop yield prediction models.⁵ Consequently, crop yield prediction in the era of global warming and climate change⁶ through the use of various ICT tools are vital for undertaking future climate action strategies.⁷

Machine learning (ML) techniques perform efficient data acquisition, model construction, and prediction in the agriculture sector.² However, when dealing with multi-dimensional datasets, the ML techniques require higher processing time, leading to poor model performance. Feature selection is a vital process in machine learning that involves choosing a subset of relevant features from a larger dataset to simplify the model and improve its performance. Feature selection plays a pivotal role⁸ in ML-based crop yield prediction. Patro et al. (2020) investigate the potential benefits of integrating machine learning algorithms with feature optimization strategy in modern agriculture was investigated.⁹ A new feature combination scheme-enhanced algorithm was proposed in this study⁹ to help optimize crop production and reduce waste through informed decisions regarding planting, watering, and harvesting crops. A novel ensemble feature selection (EFS) method was proposed to improve yield prediction from hyperspectral data.¹⁰ In this work ¹⁰,a learning framework was proposed based on the predicted values of the selected and the full features using multiple linear regressions (MLR). The results analysis proved that the optimized features achieved higher yield prediction accuracy than the full features. Also, the proposed EFS method outperformed all the individual feature selection methods across growth stages, with a mean ranging from 0.648 to 0.679. Sathya and Gnanasekaran (2023) proposed an ensemble approach to predict paddy yield accurately through feature selection techniques.¹¹ Binary cuckoo search (BCS), grey wolf optimization (GWO), and principal component analysis (PCA) have been employed over the agricultural data collected from the field and preprocessed using the Monte Carlo method.¹² The correlation coefficient of the MLR has been calculated for the data using the proposed feature selection methods for crop yield prediction.¹² Despite these advancements, traditional feature selection algorithms such as genetic algorithms (GA) often face convergence to local optima and longer computation times.¹ These limitations are addressed in this study.

Our proposed approach considers the influence of diverse environmental factors and provides predictions for crop yield. Real-time data from a private online repository (Kaggle) are utilized to both train and validate the proposed model. The Kaggle dataset splits into 60% for training and 40% for testing for comprehensive analysis. Colab (Google), an online notebook, was used to analyze the proposed model using Python coding. This study has applied an efficient feature selection strategy enhanced genetic algorithm (EGA) to perform precise yield prediction. Evaluation metrics such as mean absolute error (MAE), mean squared error (MSE), and root mean squared error (RMSE) are computed based on the selected features. A comparative analysis has been performed to justify the efficiency and accuracy of EGA over the GA in feature selection on different learning algorithms such as support vector machine (SVM), lasso regression, decision tree (DT), random forest (RF), and gradient boosting (GB). This study contributes to agricultural data science and helps farmers make informed decisions, leading to productivity and sustainability.

Proposed Scheme

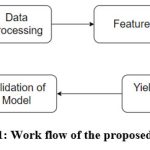Figure 1: Work flow of the proposed scheme. Click here to view Figure

Figure 1 illustrates the workflow of our proposed scheme. We leverage real-time data from a private online repository, specifically Kaggle, to train and validate the proposed scheme. Data processing ¹³ is crucial in developing machine learning-based prediction models. It involves several essential steps to prepare raw data for effective modeling. Once processed, the dataset undergoes scaling or transformation for modeling purposes.¹⁴ Subsequently, we have employed 60:40 ratios for training and validation of the proposed scheme. Here, we have implemented a feature optimization strategy to identify the most optimum features that affect crop yield production. Figure 2 illustrates the process flow of evaluating and validating the optimized feature selection scheme. It begins with data collection and preprocessing, followed by exploratory data analysis. The next step involves a standard GA optimization to select the most relevant features. If the GA yields an unstable or poor fitness score, the selection process shifts towards the EGA optimization technique. After selecting optimum features and target values using EGA, the model proceeds to make predictions and validate using various ML-based regression techniques. This structured approach (Figure 2) ensures enhanced accuracy and robustness of the crop yield predictions through optimal feature selection. The following subsection provides a detailed explanation of the optimal feature selection scheme.

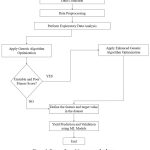Figure 2: Process flow of the proposed scheme. Click here to view Table

Optimal Feature Selection 

Features selection¹⁵ is the process of choosing the most optimal subset of features for exploration and analysis. Adaptive heuristic search algorithms are the process of natural selection that serves as the foundation for genetic algorithm (GA). The GA, inspired by biological evolution, is used to find optimal solutions to problems by mimicking the process of natural selection.¹⁶ Hence, it mimics the “survival of the fittest” among people from successive generations to address an issue.¹⁶ The GA begins by randomly placing individuals, representing potential feature combinations.¹⁶ However, this random initialization can be inefficient for several reasons. Firstly, it may scatter the search, especially in datasets with numerous features. Secondly, without any initial direction, the GA might waste considerable time exploring irrelevant areas, thus delaying the discovery of optimal solutions. Additionally, the inherent “survival of the fittest” mechanism of GA can lead to premature convergence. It severely limits efficiency and leads to the loss of diversity in the population. Hence, this study presents an enhanced genetic algorithm (EGA) to overcome these limitations.

Enhanced Genetic Algorithm (EGA)

Enhanced genetic algorithms (EGA) are evolutionary-inspired search strategies that aid in identifying the best answers in machine learning, especially for feature selection.¹⁷ EGA incorporates additional techniques to overcome the limitations of GA and enhance the overall feature optimization process.

Initialization with Latin Hypercubes Sampling (LHS)

A technique for creating a collection of samples from a multidimensional distribution is called latin hypercube sampling (LHS).¹⁸ LHS is used in the EGA to initialize the population with a wide range of potential solutions. LHS ensures a more even spread of possible feature combinations.

Preservation of the Elite

Elite preservation¹⁹ is the practice of holding onto the top performers without making any changes from one generation to the next. It keeps the pool of high-quality solutions and stops the algorithm from regressing to lower-quality answers. EGA includes a mechanism to preserve a small portion of the top-performing individuals (10% elites) from each generation. This process safeguards valuable genetic material (effective feature combinations) and reduces the risk of losing them due to the randomness of selection.

The feature selection using EGA is represented mathematically in the next sub section.

Mathematical Model

Let ‘p’ be the initial population of size , where each individual ‘p_i’(i = 1,2,…N) is a binary vector of length (the number of features). Each vector is generated randomly is expressed in equation.1.

The initialization can also be enhanced using techniques like LHS for diversity. This method ensures a more evenly distributed initial set of solutions across the search space. In this study, feature selection process using LHS, sampling a feature subset from a distribution with cumulative distribution function is represented in equation 2.

 In equation.2, ’U’ represents a uniform random number in the (N_i=1, N_i) interval for the interval out of ‘N’ total interval.

A function that evaluates the performance of each feature is known as fitness function. It defines the accuracy of the selected features. Mathematically, the accuracy can be expressed in equation 3.

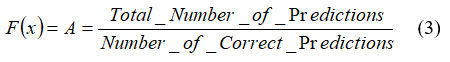
Individual features are selected based on their fitness. A common approach is the roulette wheel selection, where the probability of selecting individual ‘p_i’ is proportional to its fitness as shown in equation.4.

Where, Select(♦) is a selection function that operates over population ‘P’  and their fitness scores ‘f’ . Individual features are now selected from the population based on their fitness value through roulette wheel selection. In this method, features with higher fitness values have a higher probability of being chosen. However, the elite preservation method has been considered in EGA to enhance the feature selection method as compared to GA. To incorporate elite best feature selection into the formation of the new population P^/ from offspring ‘C’ and potentially some individuals from the current population ‘P’ , the replacement function ‘R’ is employed. This function ensures that the best-performing individuals from both populations are preserved for the next generation. Mathematically, the formation of P^/ can be written as equation 5.

This technique identifies and saves the top individuals those with the highest fitness scores without undergoing crossover or mutation operations.¹⁷ Crossover combines features from two parent individuals to create offspring. Let ‘p₁’ & ‘p₂’ be two parent individuals, and ‘C_i’ & ‘C₂’ the offspring. A crossover point ‘K’ is chosen at random, and the offspring are created as follows:

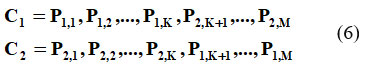
In equation 6, ‘M’ is the number of features. Now, Mutation is applied to individual (P₁, P₂,….,P₁) with a fixed mutation rate where a random bit in their chromosome is flipped. The following condition need to be followed in order to perform mutation.

If random number ≤ mutation rate, flip the bit

The potential processing time is (N x M) where ‘N’ denotes the population size a ‘M’ refers to the features used during mutation process.

At the end of the EGA process, the best features subset (P_{_best}) is selected based on the highest fitness score. This mathematical model outlines the steps and processes involved in the EGA for feature selection. Evaluation and validation of the selected features are analyzed in the next section.

Results

This section evaluates the performance of the proposed scheme and analyzes performance of the same graphically using various prediction models.

Evaluation of Feature Selection Strategy  

Table 1 compares the performance of a GA with an EGA across different metrics. The average fitness score measures the suitability or effectiveness of the chosen features. It shows that the EGA outperforms the standard GA, with scores of 0.147 and 0.012, respectively. This result indicates that the EGA is a better optimizer than the GA. EGA chooses a broader range of features, including humidity, soil pH, and several nutrient concentrations, such as soil organic carbon, nitrogen, phosphorus, and boron. However, the GA chooses fewer features, primarily focusing on temperature and concentrations of potassium and sulfur. The extensive feature set in the EGA may contribute to its higher fitness scores. The best fitness score further supports this conclusion, with the EGA achieving a top score of 0.161 compared to the GA’s 0.014.

Table 1: Comparison of optimization methods.

Metrics	Genetic algorithm	Enhanced genetic algorithm
Average fitness score	0.012	0.147
Selected features	Temperature, Potassium Concentration, Sulphur Concentration	Temperature, Humidity, Soil PH, Soil Organic Carbon Concentration, Nitrogen Concentration, Phosphorus Concentration, Boron Concentration
Best fitness	0.014	0.161

Figure 3: Analysis of fitness score for Genetic Algorithm Click here to view Figure

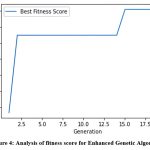Figure 4: Analysis of fitness score for Enhanced Genetic Algorithm Click here to view Figure

Figure 3 shows significant variability in fitness scores of GA across generations. The graph (Figure 3) shows sharp peaks and valleys, indicating that the best solutions are not consistently improving. Hence, it signifies that either the GA belongs in local optima or the mutation rate may be causing instability. Figure 4 shows a fitness pattern for EGA. After an initial drop, there’s a rapid improvement in the fitness score from the 5th generation onwards with relatively stable. It indicates that the EGA quickly finds a good solution and refines it through subsequent generations. Overall, the EGA appears to provide more consistent and improved performance over the GA, with less volatility in fitness scores. It leads to a more stable convergence of better solutions through the generations.

The following subsection validates the selected feature set using both algorithms.

Validation of the Selected Feature Set

This subsection conducts a comparative analysis of learning-based regression models using the selected feature set. Three distinct evaluation metrics are employed: mean absolute error (MAE), mean squared error (MSE), and root mean squared error (RMSE)²⁰ to evaluate the effectiveness. These metrics are calculated mathematically for the comprehensive result of the model’s performance.

MAE quantifies the absolute differences between predicted values and actual observations, while MSE calculates the average of the squared differences between predictions and actual values.²⁰ Consequently, MSE is more sensitive to outliers than MAE because it amplifies the differences by squaring them. These evaluation metrics are mathematically expressed as follows:

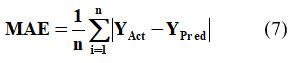
In equation 7 ‘n’ depicts the number of errors, Σ depicts the summation of all values, and |Y_Act – Y_Pred| is the absolute errors. The equation 7 can be rewritten as:

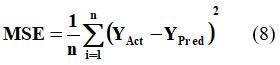
RMSE, another key evaluation metric, is defined as the square root of the MSE.²⁰ This metric involves squaring the prediction errors before averaging, which assigns greater weight to larger errors.²¹ Equation 9 provides the mathematical formulation of RMSE.

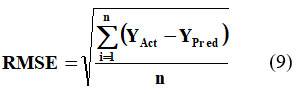
Table 2: Mean error and accuracy of different learning models

Learning algorithms	MSE		MAE		RMSE		Accuracy (%)
	GA	EGA	GA	EGA	GA	EGA	GA	EGA
SVM	1.267	1.073	0.920	0.832	1.125	1.036	48.114	69.111
Lasso	1.274	1.160	0.923	0.868	1.128	1.077	39.609	61.011
DT	1.091	0.981	0.881	0.717	1.111	0.961	56.112	86.112
RF	1.031	0.584	0.823	0.623	1.012	0.911	59.018	91.012
GB	0.962	0.534	0.796	0.511	0.981	0.899	71.871	93.009

support vector machine (SVM); decision tree (DT); random forest (RF); gradient boosting; mean squared error (MSE); mean absolute error (MAE); root mean squared error (RMSE); genetic algorithm (GA); enhanced genetic algorithm (EGA).

Table 2 compares popular learning algorithms, such as support vector machine (SVM), lasso, decision tree (DT), random forest (RF), and gradient boosting (GB), using two feature selection methods – GA and EGA. Across all models and metrics (MSE, MAE, RMSE, Accuracy), EGA consistently outperforms GA, suggesting that EGA more effectively identifies and utilizes influencing features. The efficient feature selection leads to better model accuracy and lower error rates. For instance, with SVM, accuracy improves significantly from 48.114% under GA to 69.111% with EGA. This pattern is evident in all models, with RF also showing a pronounced improvement (an accuracy boost from 59.018% to 91.012%). These results validate the superiority of EGA over GA in enhancing the predictive performance of various models by selecting more relevant features, leading to higher accuracy and reduced prediction errors across diverse learning algorithms. In Table 2, the EGA features set enabled the GB algorithm to achieve maximum accuracy. In Figure 5, we present the convergence analysis of the GB algorithm for both training and testing data sets selected and processed by EGA.

Figure 5 shows that the training data (first 2500 data points) exhibits a significant overlap between the actual yields (blue) and the predicted yields (green), indicating accurate model fitting. Similarly, the testing data (last 500 data points) displays close alignment between actual (red) and predicted (orange) yields, suggesting good generalization to unseen data. The performance of prediction accuracy across both datasets highlights the effectiveness of the EGA in selecting relevant features, thereby enhancing the model’s accuracy and reliability.

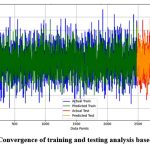Figure 5: Convergence of training and testing analysis based on EGA Click here to view Figure

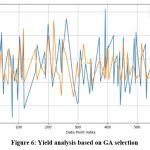Figure 6: Yield analysis based on GA selection Click here to view Figure

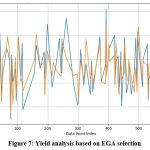Figure 7: Yield analysis based on EGA selection Click here to view Figure

Figure 6 and Figure 7 represent the convergence of actual and predicted crop yields. Figure 7 shows a closer alignment between the actual (blue) and predicted (orange) crop yields, indicating a more accurate prediction model. The fluctuations in the predicted values closely follow the actual yield trends, suggesting that the EGA effectively captures the underlying patterns in the data. In contrast, Figure 6 shows a more significant deviation between the actual and predicted values, particularly in some segments where the orange line diverges notably from the blue line. The graphical analysis indicates that the EGA is more precise than the standard GA in predicting yields. Overall, the comparison illustrates that the EGA provides superior predictive performance, likely due to better feature selection and parameter optimization, leading to more reliable yield predictions for agricultural modeling in any soil type.

Discussion   

The paper effectively justifies the importance of crop yield prediction models for agricultural planning and food security by highlighting how precise predictions enable better resource management, risk mitigation, and agricultural decision-making. Accurate yield forecasts are crucial for ensuring food security and economic stability, particularly in the face of increasing global food demand driven by population growth. The paper underscores the significance of optimized feature selection using an EGA in improving prediction accuracy and efficiency, thereby supporting sustainable and efficient agricultural management. Through a detailed comparative analysis between standard GA and EGA, the paper convincingly argues the necessity of feature optimization for enhancing model performance. It demonstrates how EGA, with techniques like Latin Hypercube Sampling (LHS) and elite preservation, addresses the limitations of traditional GAs, such as local optima convergence and high computation times. The results show significant improvements in model accuracy and reductions in error metrics (MSE, MAE, RMSE) across various machine learning models (SVM, Lasso, DT, RF, GB) when using EGA. Quantitative metrics and graphical analyses further support the argument, highlighting how EGA’s optimized feature selection leads to better predictive performance. This enhanced performance directly impacts agricultural planning and management strategies, ensuring more reliable and informed decisions for crop production.

Conclusion       

In this paper, we have demonstrated that the EGA significantly optimizes feature selection and enhances model performance for crop yield prediction. The results indicate that EGA outperforms standard GA across various evaluation metrics and learning algorithms, leading to higher accuracy and reduced error rates. For instance, EGA boosts the yield prediction accuracy of GB model from 71.871% to 93.009% and reduced the mean square error from 0.962 to 0.534. This findings validate the effectiveness of EGA in improving predictive accuracy and computational efficiency. Future work could explore integrating additional machine learning techniques with EGA to refine prediction models. Furthermore, applying the EGA approach to other agricultural datasets and crop types could provide broader insights and validate its generalizability.

Acknowledgment

We express sincere gratitude towards the Heritage Institute of Technology, Kolkata for providing the research environment and resources that enabled me to undertake this study.

Funding Sources

The author(s) received no financial support for the research, authorship, and/or publication of the article.

Conflict of Interest

The authors do not have any conflict of interest.

Data Availability Statement

This statement does not apply to this article.

Ethics Statement

This research did not involve human participants, animal, subjects, or any material that requires ethical approval.

Informed Consent Statement

This study did not involve human participants, and therefore, informed consent was not required.

Author’s Contribution

Sabyasachi Chatterjee contributes to the conceptualization, methodology, and validation of this work. He was also involved in writing and revising the manuscript.

Swarup Kumar Mondal contributes to the investigation and the development of the enhanced genetic algorithm used in this study.

Anupam Datta was responsible for data curation, software implementation, and formal analysis.

Hritik Kumar Gupta was involved in the visualization and data analysis.

All authors reviewed and approved the final version of the manuscript.

References

1. Lobell, D. B., Asseng, S. Comparing estimates of climate change impacts from process-based and statistical crop models. Environmental Research Letters.2017;12(1):015001. https://dx.doi.org/ 10.1088/1748-9326/aa518a.
   CrossRef
2. Van Klompenburg, T., Kassahun, A., Catal, C. Crop yield prediction using machine learning: A systematic literature review. Computers and Electronics in Agriculture. 2020;177: 105709. https://doi.org/10.1016/j.compag.2020.105709.
   CrossRef
3. Cedric, L. S., Adoni, W. Y. H., Aworka, R., Zoueu, J. T., Mutombo, F. K., Krichen, M., Kimpolo, C. L. M. Crops yield prediction based on machine learning models: Case of West African countries. Smart Agricultural Technology.2022; 2:100049. https://doi.org/10.1016/j.atech.2022.100049.
   CrossRef
4. Gupta, S., Geetha, A., Sankaran, K. S., Zamani, A. S., Ritonga, M., Raj, R., Mohammed, H. S. Machine learning-and feature selection-enabled framework for accurate crop yield prediction. Journal of Food Quality. 2022:1-7. https://doi.org/10.1155/2022/6293985.
   CrossRef
5. De, S. Crop Prediction Expert System with Ensemble Machine Learning Technique. In International Conference on Machine Learning, Deep Learning and Computational Intelligence for Wireless Communication. 2023:423-433. DOI: 10.1007/978-3-031-47942-7_36.
   CrossRef
6. Chowhan, S., Ghosh, S. R., Chowhan, T., Hasan, M. M., & Roni, M. S. (2016). Climate change and crop production challenges: An overview. Research in Agriculture Livestock and Fisheries. 3(2):251-269. https://doi.org/10.3329/ralf.v3i2.29346.
   CrossRef
7. Chowhan, S., & Ghosh, S. R. (2020). Role of ICT on agriculture and its future scope in Bangladesh. Journal of Scientific Research and Reports. 26(5):20-35. https://doi.org/10.9734/jsrr/2020/v26i530257
   CrossRef
8. P. S., M. G.,R., B. Performance Evaluation of Best Feature Subsets for Crop Yield Prediction Using Machine Learning Algorithms. Applied Artificial Intelligence, 2019; 33(7): 621–642. https://doi.org/10.1080/08839514.2019.1592343.
   CrossRef
9. Patro, K. K., Jaya Prakash, A., Jayamanmadha Rao, M., & Rajesh Kumar, P. An Efficient Optimized Feature Selection with Machine Learning Approach for ECG Biometric Recognition. IETE Journal of Research. 2020; 68(4):2743–2754. https://doi.org/10.1080/03772063.2020.1725663.
   CrossRef
10. Fei, S., Li, L., Han, Z., Chen, Z., Xiao, Y. Combining novel feature selection strategy and hyperspectral vegetation indices to predict crop yield. Plant Methods. 2022; 18(1):119. https://doi.org/10.1186/s13007-022-00949-0.
    CrossRef
11. Sathya, P., Gnanasekaran, P. Ensemble Feature Selection Framework for Paddy Yield Prediction in Cauvery Basin using Machine Learning Classifiers. Cogent Engineering. 2023:10(2). https://doi.org/10.1080/23311916.2023.2250061.
    CrossRef
12. Surianarayanan, C., Palanivel, K. Feature Selection for Crop Yield Prediction Using Optimization Techniques. Webology. 2029:16(2).
13. Chauhan, S., Singh, M., Aggarwal, A. K. Data science and data analytics: artificial intelligence and machine learning integrated based approach. Data science and data analytics: opportunities and challenges. 2021:1. ISBN: 9781003111290.
    CrossRef
14. Burrell, J. How the machine ‘thinks’: Understanding opacity in machine learning algorithms. Big Data & Society 2016: 3(1). https://doi.org/10.1177/2053951715622512.
    CrossRef
15. Rostami, M., Berahmand, K., Forouzandeh, S. A novel community detection based genetic algorithm for feature selection. Journal of Big Data. 2021; 8(1):2. https://doi.org/10.1186/s40537-020-00398-3.
    CrossRef
16. Babatunde, O. H., Armstrong, L., Leng, J., Diepeveen, D. A Genetic Algorithm-Based Feature Selection. International Journal of Electronics Communication and Computer Engineering. 2014; 5(4):899-905.
17. M. Abdelkhalek, A., Mohammed, A., Attia, M., Badra, N. An Enhanced Genetic Algorithm using Directional-Based Crossover and normal mutation For Global Optimization Problems. Statistics, Optimization & Information Computing. 2023; 12(2):446-462. https://doi.org/10.19139/soic-2310-5070-1796.
    CrossRef
18. Feng, Z. K., Niu, W. J., Jiang, Z. Q., Qin, H., & Song, Z. G. Monthly operation optimization of cascade hydropower reservoirs with dynamic programming and Latin hypercube sampling for dimensionality reduction. Water Resources Management. 2020; 34:2029-2041. https://doi.org/10.1007/s11269-020-02545-0.
    CrossRef
19. Zhong, Z., Jiang, H., & Zuo, H. (2024). An optimization method of electrostatic sensor array based on Kriging surrogate model and improved non-dominated sorting genetic algorithm with elite strategy algorithm. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering. 2024; 238(2):198-210. https://doi.org/10.1177/0954410023121994.
    CrossRef
20. Jierula A, Wang S, OH T-M, Wang P. Study on Accuracy Metrics for Evaluating the Predictions of Damage Locations in Deep Piles Using Artificial Neural Networks with Acoustic Emission Data. Applied Sciences. 2021; 11(5):2314. https://doi.org/10.3390/app11052314.
    CrossRef
21. Hodson, T. O. Root mean square error (RMSE) or mean absolute error (MAE): When to use them or not. Geoscientific Model Development Discussions. 2022; 14(15):5481-5487. https://doi.org/10.5194/gmd-15-5481-2022.
    CrossRef